Dynamical Systems Math Biology Janani Ravi Inside dynamical systems and the mathematics of change bryna kra explains how to describe complex systems in symbols. Comments 24 description inside dynamical systems and the mathematics of change 1.1klikes 41,750views 2020nov 17.

Modern Introduction To Dynamical Systems For Physics Mathematics And Once the idea of the dynamical content of a function or di erential equation is established, we take the reader a number of topics and examples, starting with the notion of simple dynamical systems to the more complicated, all the while, developing the language and tools to allow the study to continue. Introduction the main goal of the theory of dynamical system is the study of the global orbit structure of maps and flows. in these notes, we review some fundamental concepts and results in the theory of dynamical systems with an emphasis on diferentiable dynamics. Lecture 11: dynamical systems 11.1. dynamical systems theory is the science of time. if time is continuous, the evolution is de ned by a di erential equation x = f(x). if time is discrete, then we look at the iteration of a map x ! t (x). here is the prototype of a di erential equation in three dimensions:. Welcome to the undergraduate seminar on arithmetic dynamics! in this seminar, we will study a relatively new mathematical subject at the intersection of dynamical systems and number theory. this area of mathematics involves a breadth of mathematical disciplines, including: complex analysis p adic analysis analytic number theory algebraic number theory algorithmic number theory algebraic.

Dynamical Systems Stability Symbolic Dynamics And Chaos Studies In Lecture 11: dynamical systems 11.1. dynamical systems theory is the science of time. if time is continuous, the evolution is de ned by a di erential equation x = f(x). if time is discrete, then we look at the iteration of a map x ! t (x). here is the prototype of a di erential equation in three dimensions:. Welcome to the undergraduate seminar on arithmetic dynamics! in this seminar, we will study a relatively new mathematical subject at the intersection of dynamical systems and number theory. this area of mathematics involves a breadth of mathematical disciplines, including: complex analysis p adic analysis analytic number theory algebraic number theory algorithmic number theory algebraic. We may regard (1.1) as describing the evolution in continuous time t of a dynamical system with nite dimensional state x(t) of dimension d. els of systems whose laws do not change in time. they are invariant under translations in time: if x(t) is a so ution, then example 1.1. the lorenz system for (x; y; z) 2 r3 is xt =. The questions we will answer in this chapter are: 1. what is a differential equation? 2. what is the order of a differential equation? 3. what is an ordinary differential equation (ode)? 4. what is the time scale of change for a dynamical system? 5. what is the general form of the solution of an n th order linear ode with constant coefficients?.

Dynamical Systems Theory Intechopen We may regard (1.1) as describing the evolution in continuous time t of a dynamical system with nite dimensional state x(t) of dimension d. els of systems whose laws do not change in time. they are invariant under translations in time: if x(t) is a so ution, then example 1.1. the lorenz system for (x; y; z) 2 r3 is xt =. The questions we will answer in this chapter are: 1. what is a differential equation? 2. what is the order of a differential equation? 3. what is an ordinary differential equation (ode)? 4. what is the time scale of change for a dynamical system? 5. what is the general form of the solution of an n th order linear ode with constant coefficients?.

Dynamical Systems Theory Wikipedia

Differential Dynamical Systems Cambridge University Press Assessment
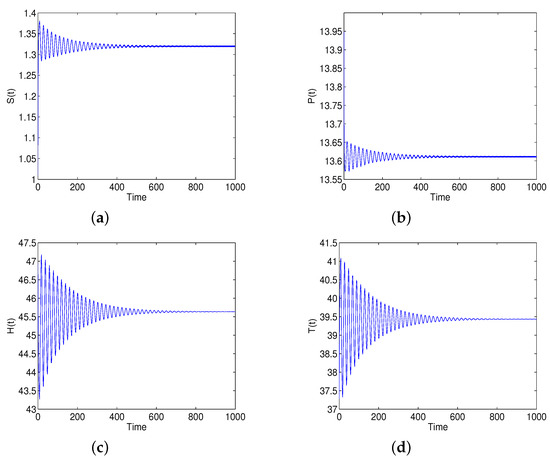
Mathematics Special Issue Recent Advances In Theory And Application