
Unit 1 1 Class Eigenvalue Eigenvector Method Pdf Shows the entire solution process of a 2 variable system using characteristic equation, eigenvalues, and eigenvectors. [1] eigenvectors and eigenvalues example from di erential equations consider the system of rst order, linear odes. dy1 = 5y1 2y2 dt dy2 = 2y1 5y2 dt.

7 3 Eigenvalue Method For Linear Systems Download Free Pdf In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. suppose we have such a system. Matrix methods for solving systems of 1st order linear differential equations the main idea: given a system of 1st order linear differential equations d x dt = ax with initial conditions x (0) , we use eigenvalue eigenvector analysis to find an appropriate basis b = { v 1 , , vn } for rn and a change of basis matrix. Practice and master eigenvalues and eigenvectors with our comprehensive collection of examples, questions and solutions. our presentation covers basic concepts and skills, making it easy to understand and apply this fundamental linear algebra topic.

Solved Find The Eigenvalue о о An Eigenvector Vвѓ 1vв 1 And A Chegg Matrix methods for solving systems of 1st order linear differential equations the main idea: given a system of 1st order linear differential equations d x dt = ax with initial conditions x (0) , we use eigenvalue eigenvector analysis to find an appropriate basis b = { v 1 , , vn } for rn and a change of basis matrix. Practice and master eigenvalues and eigenvectors with our comprehensive collection of examples, questions and solutions. our presentation covers basic concepts and skills, making it easy to understand and apply this fundamental linear algebra topic. A guide to solving linear systems the key to solving linear systems is to nd eigenvalues and eigenvectors for the matrix. if a is a square matrix, then we say is an eigenvalue for a if there is a non zero vector ~v so that a~v = ~v. we call ~v an eigenvector for a and . Least squares solving the most general and accurate method to solve under or over determined linear systems in the least squares sense, is the svd decomposition. eigen provides two implementations. the recommended one is the bdcsvd class, which scales well for large problems and automatically falls back to the jacobisvd class for smaller problems.
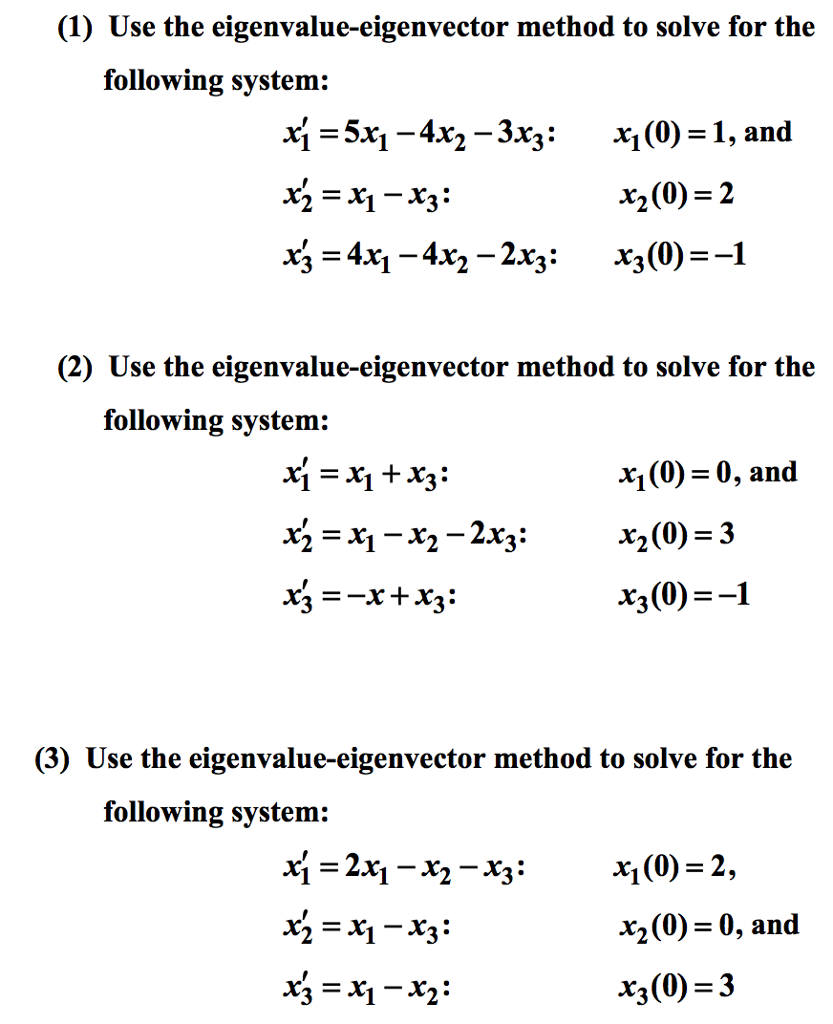
Solved 1 Use The Eigenvalue Eigenvector Method To Solve Chegg A guide to solving linear systems the key to solving linear systems is to nd eigenvalues and eigenvectors for the matrix. if a is a square matrix, then we say is an eigenvalue for a if there is a non zero vector ~v so that a~v = ~v. we call ~v an eigenvector for a and . Least squares solving the most general and accurate method to solve under or over determined linear systems in the least squares sense, is the svd decomposition. eigen provides two implementations. the recommended one is the bdcsvd class, which scales well for large problems and automatically falls back to the jacobisvd class for smaller problems.

Solved 1 Use The Eigenvalue Eigenvector Method To Find Chegg

Solved 2 Points Consider The Initial Value Problem Ys Y0 2